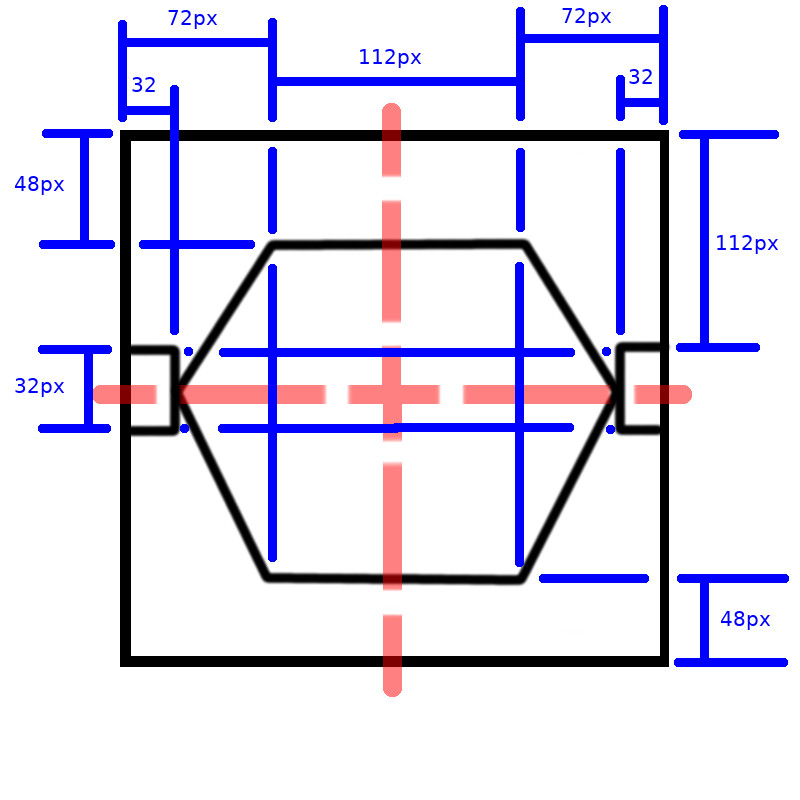
The black box represents the 256x256 viewport
Last modified: 2021.07.25
The first thing to talk about would obviously be the idea for the spinning hexagon itself. I just had the idea to make something like this and I thought it would look cool. There's not much of a story to that part, but the idea for how to implement it here has more substance to it. Canvas is really only designed to do 2D graphics, so just making a 3D hexagon and animating it wasn't really an option.
However, canvas has functions for drawing lines and line segments of varying widths. By using two lines, each comprised of three lines segments, the lines can move and change width independently of each other while still looking like a single six-sided figure. To create the illusion that it's spinning, the lines will need to change position, with their width changing accordingly.
One line will start closer to the top of the frame and move towards the bottom, while the other starts near the bottom and moves towards the top. As they move towards the center, one line will need to get wider while the other gets narrower. The opposite process will need to occur as they move away from the center.
These lines are being drawn in a canvas that is 256 pixels wide and 256 pixels tall. I wanted a relatively small size for the canvas so that it wouldn't take up too much space on a screen. It also helps that 256 is a nice binary number (100000000) that turned out to be a good choice later in the process.
I didn't want the hexagon to take up the entire canvas, so I decided to add some blocks to the left and right sides to make it look like they were "holding" the sides of the hexagon. Each of these blocks were made to be 32 pixels by 32 pixels, centered along the Y-axis, with one on both the left and right sides of the canvas. This occupies 64 pixels (2*32) of the 256 pixels of width along the canvas, leaving 192 pixels left.
Both lines have two segments that run diagonally from the blocks on the sides to a third, flat line segment. The X coordinates for where the flat segment joins up with the other two can be hard-coded to whatever value looks right, which I decided was 40 pixels away from the block. The Y coordinates would be determined by where in the animation the lines are at. They can start at a value that looks right (in this case, 48 pixels from the top/bottom of the canvas) and a displacement can be calculated based on which frame of the animation it's at.

When the two lines make it to the opposite end from where they started, they will be in the position that the oppsite line started in. To simplify the logic that makes this animation happen, the position of the lines can be reset just before reaching that point. This will make it look like the lines make it to the other side while it actually sends the lines back to where they started, creating a seamless animation loop. This introduces limitations to how the hexagon can look while still maintaining the illusion, such as the color choice for the lines segments and the point about which the hexagon rotates.
Sticking with the theme of choosing nice binary numbers, I decided to make the number of steps between the start and end of the animation 64 steps. The rate at which these steps are performed in the browser (basically, the speed of the animation) is determined elsewhere, so this decision mostly affects how smooth the animation will look, and more importantly, the rate at which the lines need to move. There's another reason I chose it, but I'll save that for later. Earlier, I mentioned that the Y-axis positions of the lines could be determined by an offset from their starting positions. Now that there's a starting position, an ending position, and a number of steps that will be taken to move between the two, a rate can be calculated.
With the starting and ending position, the number of pixels that will need to be traveled can be calculated. The top line starts at 48px, while the bottom line starts at (256-48 = 208)px, making the distance between the two (208-48 = 160)px. The lines will need to move 160px over the course of 64 steps, making the rate at which the lines need to move (160/64 = 2.5) pixels per step. The offset can then be calculated by multiplying the current step (number between 0 and 63) with this rate, which can then be used to find where the line should go.
JavaScript stores numbers as floating point values, so there's no issue with multiplying that 2.5 by the numbers that could otherwise be stored as integer values. When writing the code originally, I didn't know that, so I made a way for the math to work without having to use floating point numbers. Even though it's not necessary for this hexagon to work, working with floating point numbers affects the performance of programs, so if there's a way to make part of a program work without using floats in a language that actually has integer values, it's preferable to avoid using the floats.
With that said, I still didn't know about the lack of integer values in JavaScript at the time of writing, so here's how I got that 2.5 multiplied by the current step. When saying "2.5", one way it can be stated is as "two and a half". The reason I'm mentioning this is because 2.5 can be broken down into the sum of 2 and 0.5 (2.5 = 2 + 0.5). Oh boy, it's algebra time. By extension, 2.5 multiplied by the current step (which I'll represent using 's') can be broken into (2.5*s = 2*s + 0.5*s = 2*s + s/2).
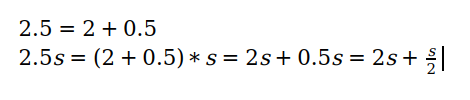
When dividing two integer values, the result will be truncated to an integer value. For example, dividing 3 by 2 will result in 1.5, which will then be truncated to 1. Instead of moving at a steady rate of 2.5 pixels for each step, the lines will alternate between moving two pixels and three pixels per step. As long as this is done with a sufficient speed and number of pixels, the difference will be difficult, maybe even outright impossible, for anyone to notice.
Using division can introduce performance detriments. This explanation is long enough without getting into why that is and talking about bit shifts, so I'll just say that dividing by two is relatively easy for computers to do, so that won't be a problem. With that out of the way, I'll move on to how these ideas got implemented in the code.
Next page: The Code Behind the Spinning Hexagon
Previous page: Ruin the Rotating Hexagon Illusion
Back to main page